From hours to 360ms: over-engineering a puzzle solution

In January 2025, Jane Street posted an interesting puzzle:

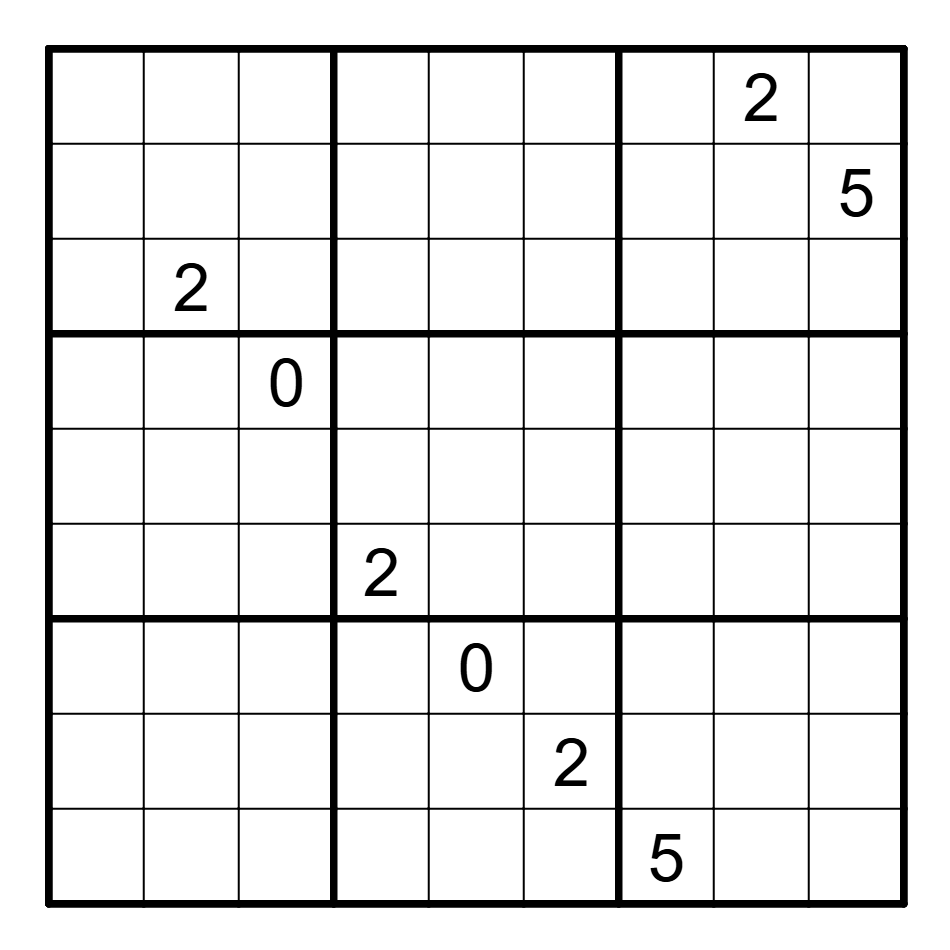
Fill the empty cells in the grid above with digits such that each row, column, and outlined 3-by-3 box contains the same set of nine unique digits (that is, you’ll be using nine of the ten digits (0-9) in completing this grid), and such that the nine 9-digit numbers (possibly with a leading 0) formed by the rows of the grid has the highest-possible GCD over any such grid.

Some of the cells have already been filled in. The answer to this puzzle is the 9-digit number formed by the middle row in the completed grid.

Cheesing

My first attempt when solving this puzzle was to encode the constraints as an SMT optimization problem, and using Z3 to find the solution.

Unfortunately, even after leaving this running for several hours, no solution was found.

Back to math class

Instead of leaving everything to a computer, some observations can be made:

Label the GCD of all rows as $x$ , and the number in each row as $r_{i}$ with $i$ between 1 and 9. Then, following the rules of the puzzle:

Each row $r_{i}$ must be a distinct multiple of $x$ (having the same multiple show up twice repeats digits in a column, making it no longer a valid Sudoku board).
The digits of each $r_{i}$ must be distinct (any repeated digits would repeat in the same row, making it no longer a valid Sudoku board).

One observation here is that $x \leq 111111111$ . This is because maximizing $x$ requires minimizing each of $r_{i}$ , and the most that could be done is for $r_{i} = i x$ in order to keep the rows distinct. The largest row $r_{9} = 9 x \leq 999999999$ , otherwise it would overflow the 9 available digit spaces on the Sudoku board, and therefore $x = \frac{r_{9}}{9} \leq \frac{999999999}{9} = 111111111$ .

Using BFS (brute force search)

Using this observation, finding the solution with brute force could work like this:

Enumerate all possible values of $x$ in decreasing order, starting with $111111111$
Compute all multiples of $x$ where $n x \leq 999999999$ to use as possible values of $r_{i} = n x$
Run a backtracking search over the board to find a valid solution

Since the board has 9 rows, there must be at least 9 distinct multiples of $x$ that each have 9 different digits. One possible way to calculate this would be like this:

// A number is "good" if it has 9 distict digits
fn is_good(n: u32) -> bool {
    let digits: HashSet<_> = n.to_string().chars().collect();
    digits.len() == 9
}

fn multiples(x: u32) {
    (1..)
        .map(move |n| x * n)
        .take_while(|n| n <= 999999999)
        .filter(|n| is_good(*n))
}

fn has_enough_good_multiples(x: u32) -> bool {
    multiples(x).nth(8).is_some()
}

Here, has_enough_good_multiples checks multiples of $x$ and stops early if it finds the 9th "good multiple".

This works, but is quite slow, taking several minutes just to finish. Mainly, is_good requires allocating memory and hashing for each number. This can be improved by replacing a HashSet with a bitset:

fn is_good(mut n: u32) -> bool {
    let mut digits = 0u32;

    for _ in 0..9 {
        let last_digit = n % 10;
        n /= 10;
        digits |= (1 << last_digit);
    }

    assert!(n == 0);

    digits.count_ones() == 9
}

INFO

We start with a typical digit extraction loop:

for _ in 0..9 {
    let last_digit = n % 10;
    n /= 10;
    digits |= (1 << last_digit);
}

For each digit, we set the corresponding bit in our bitset. By shifting 1 (0b0000000001) left by the digit's value, each single-digit number gets mapped to a different bit in the binary representation:

digits |= (1 << last_digit);

Make sure that the number had at most 9 digits. This should always be true since multiples stops before reaching 10 digits:

assert!(n == 0);

Finally, we use count_ones to count the number of 1s in our bitset's binary representation. If there are exactly 9 bits set, it means we had 9 unique digits:

digits.count_ones() == 9

Combining this with a backtracking solve function, a solution can be found:

for x in (0..=111111111).rev() {
    if has_enough_good_multiples(x) {
        if let Some(solution) = solve(x) {
            return solution;
        }
    }
}

This finds a valid solution with $x = 12345679$ .

Too slow

With some multithreading, this can be made faster "for free":

let x = AtomicU32::new(111111111);
thread::scope(|s| {
    for _ in 0..available_parallelism().unwrap().get() {
        s.spawn(|| loop {
            let x = x.fetch_sub(1, Ordering::Relaxed);
            assert!(x > 0);
            if has_enough_good_multiples(x) {
                if let Some(solution) = solve(x) {
                    dbg!(solution);
                    exit(0);
                }
            }
        });
    }
});

However, there's still some performance improvements to be made with is_good.

Enter SIMD (Single Instruction, Multiple Data). Instead of performing operations on a single number at a time, SIMD allows processing of multiple numbers with a single operation:

fn is_good(mut x: u32) -> bool {
    if x > 999999999 {
        return false;
    }

    let a = x / 1000000;
    let b = (x / 1000) % 1000;
    let c = x % 1000;

    let d = Simd::from_array([a, b, c, 0]);

    let d0 = d % Simd::from_array([10, 10, 10, 10]);
    let d1 = (d / Simd::from_array([10, 10, 10, 10])) % Simd::from_array([10, 10, 10, 10]);
    let d2 = (d / Simd::from_array([100, 100, 100, 100])) % Simd::from_array([10, 10, 10, 10]);

    let e0 = Simd::from_array([1, 1, 1, 0]) << d0;
    let e1 = Simd::from_array([1, 1, 1, 0]) << d1;
    let e2 = Simd::from_array([1, 1, 1, 0]) << d2;

    let f = e0 | e1 | e2;

    let g = f.reduce_or();

    g.count_ones() == 9
}

INFO

The first step is to eliminate numbers that are too large:

if x > 999999999 {
    return false;
}

Start by splitting x into 3 groups of digits, with each group having 3 digits each:

let a = x / 1000000;
let b = (x / 1000) % 1000;
let c = x % 1000;

Now we can start using SIMD. A SIMD value (or a "vector") contains multiple numbers that operations can be applied to simultaneously.

Details

In many scenarios, the exact same operation gets applied to a bunch of numbers. Consider the following loop:

for i in 0..list.len() {
    list[i] *= 2;
}

This would do the same thing for every number in list. But using SIMD can make this work faster:

// Pseudocode
for i in 0..list.len().step_by(16) {
    list[i..i + 16] *= [2; 16];
}

In the above pseudocode, list[i..i + 16] would be a 16-dimensional vector, and multiplying by [2; 16] (another 16-dimensional vector) would multiply element-wise.

Real code using SIMD wouldn't look exactly like this — in Rust, each vector uses the Simd type.

Create a vector with our three groups, plus a padding zero to fit nicely into a 4-valued vector:

let d = Simd::from_array([a, b, c, 0]);

Next, extract digits from all 3 groups at once. We get the ones digit (d0), tens digit (d1), and hundreds digit (d2) from each group:

let d0 = d % Simd::from_array([10, 10, 10, 10]); // The ones digit
let d1 = (d / Simd::from_array([10, 10, 10, 10])) % Simd::from_array([10, 10, 10, 10]); // The tens digit
let d2 = (d / Simd::from_array([100, 100, 100, 100])) % Simd::from_array([10, 10, 10, 10]); // The hundreds digit

For each group, perform a bitshift. The fourth padding zero in each vector is ignored:

let e0 = Simd::from_array([1, 1, 1, 0]) << d0;
let e1 = Simd::from_array([1, 1, 1, 0]) << d1;
let e2 = Simd::from_array([1, 1, 1, 0]) << d2;

Combine all the bitsets using bitwise OR operations. First, we combine the 9 individual "sets" with 1 element each:

let f = e0 | e1 | e2;

Combine the 3 "sets" that each have 3 elements:

let g = f.reduce_or();

Finally, a number is "good" if the final bitset has exactly 9 bits set to 1:

g.count_ones() == 9

This speeds up is_good quite a bit, but scalar (non-SIMD) operations still take up a large portion of the time spent.

SIMD but better

Instead of performing SIMD operations on the digits in a single number, multiple multiples (no pun intended) of $x$ can be checked at once. Replacing is_good that checks if a single number is "good" with is_good_many that checks multiple numbers and counts the amount that are "good":

fn is_good_many<const N: usize>(xs: Simd<u32, N>) -> u32
where
    LaneCount<N>: SupportedLaneCount,
{
    let mut seen = Simd::from_array([0u32; N]);

    let mut x = xs;
    for _ in 0..9 {
        let after_div = x / Simd::splat(10);
        let last_digit = x - (after_div * Simd::splat(10));
        let mask = Simd::from_array([1u32; N]) << last_digit;
        seen |= mask;
        x = after_div;
    }

    let unseen = Simd::from_array([0b1111111111; N]) - seen;
    let unseen: Simd<f32, N> = unseen.cast();
    let unseen = unseen.to_bits();

    let bad = Simd::splat(0x7FFFFFu32) & unseen;
    let bad = bad.simd_ne(Simd::splat(0));
    let bad = bad | xs.simd_gt(Simd::splat(999999999));

    bad.select(Simd::splat(0u32), Simd::splat(1u32))
        .reduce_sum()
}

INFO

The first part follows the same logic as before — extract digits and build a bitset, but for multiple numbers at once:

for _ in 0..9 {
    let after_div = x / Simd::splat(10);
    let last_digit = x - (after_div * Simd::splat(10));
    let mask = Simd::from_array([1u32; N]) << last_digit;
    seen |= mask;
    x = after_div;
}

Details

Why is the code dividing by 10, then multiplying it back?

Well, it turns out that the most expensive operations on x86 are related to division, and calculating x / 10 along with x % 10 would do this twice!

Instead, once x / 10 is calculated, using x - (x / 10) * 10 would be faster since subtraction and multiplication would still be faster than a second modulo operation.

But here's where things change. x86 has a popcnt ("population count") instuction to count the amount of bits set to 1 in a number's binary representation. However, there isn't a SIMD equivalent — instead, we use evil floating point bit level hacking. First, get the complement of each bitset:

let unseen = Simd::from_array([0b1111111111; N]) - seen;

Then cast to floating point and extract the bits. Why? Because when a number is "good", its bitset complement will be a power of 2, which has a special property in floating point representation — its mantissa bits are all zero:

let unseen: Simd<f32, N> = unseen.cast();
let unseen = unseen.to_bits();

Details

To start, observe that a number is "good" if it has 9 distinct digits (out of 10 possible digits), which means that a "good" number would have the last 10 bits in the bitset have exactly 9 bits of 1 and 1 bit of 0. Therefore, subtracting the bitset from 0b1111111111 (1023) finds the set complement, where a "good" number has only 1 bit of 1, with the other bits all zero:

let unseen = Simd::from_array([0b1111111111; N]) - seen;

Numerically, this means that a "good" number's bitset complement must be a power of 2.

This is where floating point numbers come in. A 32-bit floating point number is stored as follows:

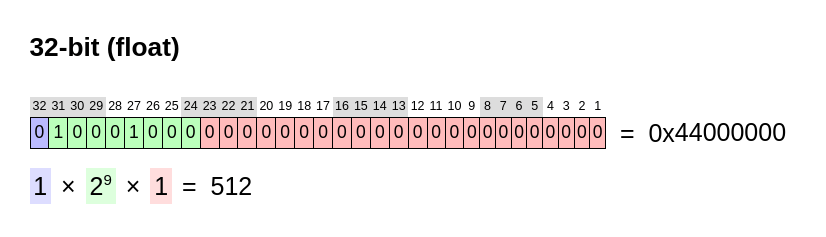
32-bit floating point number

The first bit (in blue) represents the sign of the number: 0 if the number is positive, and 1 is the number is negative.

The next 8 bits (in green) represent the exponent of the number: the 8 bits 0b10001000 (136) represent an exponent of 9 (the exponent is offset by 127, otherwise floats cannot represent numbers less than 1).

The last 23 bits (in red) represent the mantissa of the number: the 23 bits 0b00000000000000000000000 represent a number of 1.00000000000000000000000 in base 2. Since 512 is a power of 2, the mantissa is all zeros.

However, what would happen if when is_good_many sees a number that isn't "good"? The bitset would have less than 9 bits set to 1, and taking the complement would lead to more than 1 bit set to 1. But this means that the number would no longer be a power of 2. Suppose the bitset complement was 0b100101101 (301), which is not a power of 2. Then, converting 301 into a float would look like this:

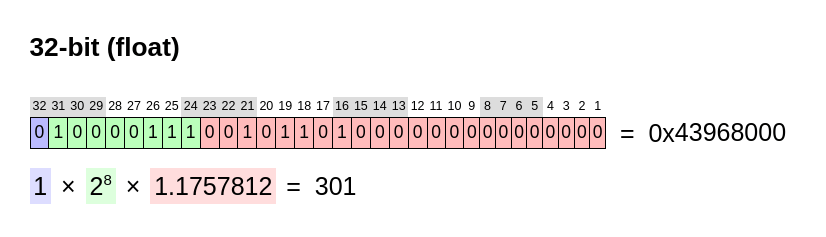
32-bit floating point number

The green exponent bits cannot represent 301 exactly (since it's not a power of 2), so the mantissa bits must be non-zero!

Checking the mantissa by masking out everything except for the mantissa bits with 0x7FFFFF:

let bad = Simd::splat(0x7FFFFFu32) & unseen;
let bad = bad.simd_ne(Simd::splat(0));

Finally, eliminate numbers that are too large and count how many good numbers we found:

let bad = bad | xs.simd_gt(Simd::splat(999999999));

bad.select(Simd::splat(0u32), Simd::splat(1u32))
    .reduce_sum()

Going back to has_enough_good_multiples — we need to change is_good to is_good_many. The old code only checks a single number at a time, but is_good_many expects chunks of multiple numbers.

The new implementation looks like this:

fn has_enough_good_multiples(n: u32) -> bool {
    const BLOCK_SIZE: usize = 16;
    const OFFSETS: [u32; BLOCK_SIZE] = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15];

    let mut count = 0;
    for offset in (0..).step_by(BLOCK_SIZE) {
        if n * offset > 999999999 {
            break;
        }
        let test =
            Simd::from_array([n; BLOCK_SIZE]) * (Simd::splat(offset) + Simd::from_array(OFFSETS));
        count += is_good_many(test);
        if count >= 9 {
            return true;
        }
    }
    false
}

This checks multiples of $n$ in groups of 16, using is_good_many instead of is_good.

Threads, leave each other alone

There's still one more slow part. Back in the main function, each thread used the same atomic variable to synchronize the value of $n$ that it checks:

let x = x.fetch_sub(1, Ordering::Relaxed);

This line dominates the time taken overall due to thread contention. As a last optimization, each thread can handle chunks of possible $n$ s on its own, using the atomic variable sparingly:

let x = AtomicU32::new(111111111);
thread::scope(|s| {
    for _ in 0..available_parallelism().unwrap().get() {
        s.spawn(|| loop {
            let x = x.fetch_sub(1024, Ordering::Relaxed); 
            assert!(x > 0);
            for x in (x - 1024)..x { 
                if has_enough_good_multiples(x) {
                    if let Some(solution) = solve(x) {
                        dbg!(solution);
                        exit(0);
                    }
                }
            } 
        });
    }
});

On a laptop with AMD Ryzen 7 7735HS with 16 threads, this code finishes in 360ms.

	Time taken	Speedup factor
Z3	Several hours, did not finish
Brute force with `HashSet`	589s	1x
Brute force with bitset	15.1s	39x
Brute force with bitset and multithreading	2.2s	267x
Brute force with SIMD and multithreading	1.5s	392x
Brute force with SIMD, chunking (`is_good_many`), and multithreading	1.3s	453x
Brute force with SIMD, chunking (`is_good_many`), and uncontended multithreading	360ms	1636x

Full source code

The real solution

Of course, none of this optimization was necessary — the puzzle's solution only needed a single number for the answer, and unlike Advent of Code, there aren't any program inputs, so a program that simply prints the correct answer would be just as valid.

But doing this shows that even though simple calculations that only involve basic arithmetic appear to have a simple and fast solution, there can still be a lot of room for improvement.

So, I guess this was the real winner all along:

	Time taken	Speedup factor
Hardcoded answer	0ms	$\infty$ x

From hours to 360ms: over-engineering a puzzle solution ​

Cheesing ​

Back to math class ​

Using BFS (brute force search) ​

Too slow ​

SIMD but better ​

Threads, leave each other alone ​

The real solution ​

All Blog Posts

From hours to 360ms: over-engineering a puzzle solution

Cheesing

Back to math class

Using BFS (brute force search)

Too slow

SIMD but better

Threads, leave each other alone

The real solution